Läuft es sich in Kinderschuhen besser? 2014
Über kompositorisches Denken mit und vor dem Computer
(Eine leicht gekürzte Fassung erschien in Band 141 der Zeitschrift MusikTexte, Köln)
Zwei Welten
Neue Musik und Elektronische Musik kommen aus zwei ganz unterschiedlichen Traditionslinien. Das, was etwas hilflos seit ungefähr hundert Jahren „Neue Musik" genannt wird, setzt - nicht zuletzt im Selbstverständnis der Komponierenden - eine jahrhunderte lange Tradition westlicher Kunstmusik fort; mit allem, was dazugehört an Kenntnis der Literatur, der Instrumente, der Notation, der früheren und gegenwärtigen Kompositionstechniken. „Elektronische", „elektroakustische" oder „Computer"musik heissen nicht zufällig nach technischen Gerätschaften: Sie sind entstanden, weil verrückte Leute aus etwas, das zu einem ganz anderen Zwecken entstanden war, Musik gemacht haben. Das betrifft die Signalgeneratoren der 50er Jahre (ursprünglich Messgeräte) ebenso wie den Computer, der als unförmige Rechenmaschine startete und als Büromaschine sein heutiges Aussehen bekommen hat.
Es ist also kein Wunder, dass viele wichtige Komponisten und Komponistinnen zeitgenössischer Musik von „der Elektronik" nicht viel wissen wollten, oder zumindest kaum etwas in diesem Medium produziert haben. Zu verschieden ist die Art, wie man in beiden Bereichen arbeitet: Schreiben und mit ausführenden, interpretierenden Menschen arbeiten hier; Beschäftigung mit und oft enormer Zeitaufwand für Technik dort.
Umgekehrt liegt es natürlich auch von seiten „der Elektronik“ aus keineswegs auf der Hand, die solcherart mit technischen Geräten erzeugte Musik mit zeitgenössischen Kompositionswerkzeugen zu produzieren.¹ Bleibt von seiten derjenigen Komponisten, die sich „mal“ mit Elektronik beschäftigen, diese oft an der Oberfläche von „interessanten Klängen“ oder „Effekten“, so verwenden diejenigen, die von der technischen Seite der Elektronik herkommen, oft musikalische Mittel, die vom Standpunkt Neuer Musik aus unreflektiert und überkommen erscheinen müssen.
Es geht aber auch anders, und dort wird es wirklich spannend. Dort, wo es zu einer inneren Beziehung der beiden - ursprünglich getrennten - Bereiche kommt. Wenn beispielsweise Nono in seiner Live-Elektronik der 80er Jahre das fortsetzt, was ihn in dieser Zeit als Komponist überhaupt interessiert: in die Klänge hinein zu gehen, Zeit zu dehnen, Dimensionen in einem Klang, und dessen Resonanzen, zu öffnen. Die Elektronik setzt das fort, sie transformiert es auf eine neue Ebene. Die Elektronik wird aber auch selber dadurch unverwechselbar geformt; sie wird aus einer Ansammlung von Geräten und Techniken zu einem wirklichen (und individuellen) Instrument.
Ich möchte hier einer anderen Art von innerer Verbindung zwischen den Bereichen "Elektronik" und "modernes Komponieren" nachgehen. Einer Verbindung, die nicht - wie so häufig - bei den Klängen ansetzt, sondern die eine Vorgehensweise, eine Art zu denken betrifft. Ich möchte an zwei paradigmatischen Stücken der frühen 50er Jahre zeigen, dass sich hier ein kompositorisches Denken ausprägt, das sich vollkommen mit dem deckt, was man tut, wenn man ein Computerprogramm schreibt. Mit anderen Worten: Komponisten "programmieren" ihre Musik -- zu einer Zeit, als die höheren Programmiersprachen erst entstehen, und ohne Kenntnis der Vorgänge in diesem Zweig der technischen Welt.²
Es geht also um den Aufweis einer fundamentalen "Verwandtschaft" zwischen der Kompositionstechnik und einem Vorgang, der dem Computer essentiell ist: dem Programmieren. Ich werde dazu zunächst kurz auf die Entwicklung des Computers, und vor allem der zum Computer führenden Denkweise eingehen. In diesem Zusammenhang soll der Begriff des Algorithmus besprochen werden. Vor diesem Hintergrund analysiere ich dann das Vorgehen von Stockhausen in Studie II und von Cage in Williams Mix. Abschließend diskutiere ich die Frage, was die spezifischen Qualitäten von Cages und Stockhausens Vorgehen als Komponisten sind: Wenn das, wie vorgegangen wird, so viele Ähnlichkeiten zu einem quasi automatischen Prozess hat, worin liegen dann die eigentlich künstlerischen Qualitäten?
Denken, Formalisieren, Computer
Elektronische Musik wird heute fast ausschließlich mit dem Computer produziert. Er hat alle früheren selbständigen technischen Einheiten (Signalgeneratoren, Bandmaschine, Filter etc. pp.) in sich aufgesogen. Woher diese Fähigkeit?
Auf der Seite des äußeren Geräts, der Hardware, ist der Prozess ebenso einfach wie langweilig zu beschreiben: Der Computer wird immer schneller, immer kleiner, immer billiger. Der ENIAC von 1946 stand auf einer Fläche von 10 X 17 Metern, wog 27 Tonnen und kostete nach heutigen Preisen etwa 5.000.000 €.³ Er hatte einen Speicher von 80 Bytes.⁴ Der IBM 7090 von 1960 kostete etwa dasselbe, hatte aber schon 150 KB Arbeitsspeicher. Der erste „Personal Computer“ HP-9100A von 1968 ließ sich schon auf einen Schreibtisch stellen; er hatte allerdings verglichen mit den Großrechnern nur wenig Speicher,⁵ kostete dafür aber auch nur etwa 70.000 €.⁶ Die im heutigen Sinne ersten „PC“s Ende der 70er Jahre hatten etwa 10 KB Speicher und kosteten um die 5.000 €.⁷
Ein heutiges „Tablet“ wiegt einige hundert Gramm, hat Gigabytes an Speicher, kann das zig-fache von früheren Großrechnern und kostet etwa 500 €.
Aber das ist nicht der Grund dafür, dass der Computer alle möglichen anderen Geräte in sich aufnehmen kann. Der Grund dafür liegt in seiner Programmierbarkeit. Diese Programmierbarkeit stellt eine neue Qualität in der Entwicklung von Maschinen dar. Sie setzt eine Formalisierung voraus, und diese Formalisierung und „Ausführbarkeit“ ist es, die eine Verbindung zwischen der programmierbaren Maschine und wichtigen Tendenzen in Neuer Musik darstellt. Für die Entstehung des Computers sind dabei Diskussionen in der Mathematik besonders bedeutsam. Auf sie soll daher kurz eingegangen werden. Sie stellen den wissenschaftsgeschichtlichen⁸ Hintergrund dar, zu dem sich manche kompositorische Verfahrensweisen in Bezug setzen lassen.
David Hilbert versuchte die Grundlagenkrise in der Mathematik zu Beginn des 20. Jahrhunderts⁹ durch einen konsequenten Selbstbezug der mathematischen Verfahrensweisen zu lösen. Es ging nicht mehr um eine Verbindung aus „unmittelbar einleuchtenden“ Axiomen und daraus abgeleiteten logischen Folgerungen,¹⁰ sondern um ein in sich selbst, quasi ohne Außenbezug, stimmiges System.¹¹ Dazu musste vor allem gezeigt werden, dass ein solches System vollständig ist,¹² und dass irgendeine Aussage in ihm entscheidbar ist.
Kurt Gödel bewies jedoch 1931, dass ein hinreichend komplexes System zwangsläufig unvollständig ist - es muss Aussagen enthalten, die sich nicht in ihm begründen lassen. „In jedem genügend reichhaltigen System lassen sich Sätze formulieren, die innerhalb des Systems weder beweis- noch widerlegbar sind, es sei denn das System wäre selbst inkonsistent.“¹³ Gödel beweist das - stark vereinfacht gesagt - durch Untersuchung des Satzes „Diese Satz ist nicht beweisbar“.¹⁴
Operierte schon dieser Beweis in merkwürdiger Weise mit Zahlen (das berühmte „gödelisieren“),¹⁵ so ging Alan Turing 1936 in On Computable Numbers, with an Application to the Entscheidungsproblem¹⁶ noch einen Schritt weiter. Er führte nämlich eine mathematische Berechnung auf eine extrem einfache Maschine zurück, die das formalisiert, was man beim Rechnen „mit der Hand“ auf Kästchenpapier macht.¹⁷ Diese Maschine kann also lesen, schreiben, und das Band nach links oder rechts transportieren.¹⁸ Durch das modellhaft-konsequente Durchspielen der möglichen Zustände, in denen sich die Maschine befinden kann, kommt Turing zu dem Schluss, dass das Entscheidungsproblem unlösbar ist:
„I propose, therefore, to show that there can be no general process for determining whether a given formula A of the functional calculus K is provable, i.e. that there can be no machine which, supplied with any one A of these formulae, will eventually say whether A is provable. “ (259) „We are now in a position to show that the Entscheidungsproblem cannot be solved. Let us suppose the contrary. Then there is a general (mechanical) process for determining whether Un is provable. By Lemmas 1 and 2, this implies that there is a process for determining whether Un ever prints 0, and this is impossible, by §8. Hence the Entscheidungsproblem cannot be solved.“ (262)
Mit anderen Worten: Ein hochabstraktes mathematisches Problem wird mit Hilfe einer (gedachten, modellierten) Maschine durchgespielt und „gelöst“.¹⁹ Einen ähnlichen Weg, zwar ohne das Gedankenmodell der Maschine, aber in einer Formulierung, die von einer Maschine verstanden werden kann, geht zur gleichen Zeit Alonso Church.²⁰ Er formalisiert mathematische und logische Operationen mit Hilfe des sogenannten Lambda Kalküls. Auch dies „with an application to the Entscheidungsproblem“: auch er bewies, dass die Hilbertsche Forderung nicht einlösbar ist.²¹ Der Lambda Kalkül aber wurde in den 50er Jahren das Grundmodell eines Zweigs der höheren Programmiersprachen.²²
Werfen wir abschließend noch einen Blick auf eine Arbeit von Claude Shannon aus dem Jahre 1938, betitelt A Symbolic Analysis of Relay and Switching Circuits. Hier geht es nicht um das Hilberprogramm, aber es wird gezeigt, dass sich logische Strukturen unmittelbar in Schaltkreise mit einfachen Ein/Aus-Schaltern abbilden lassen: "Due to this analogy any theorem of the true calculus of propositions is also a relay theorem if interpreted in terms of circuits."²³ Symbolische Logik lässt sich also elektrifizieren, und es spielt dabei keine Rolle, ob die Schalter mechanische Relais, Röhren, Transistoren oder elektronische Gatter sind.
Der Computer ist also kein Gerät wie jedes andere. Er ist Teil und materieller Ausdruck einer fundamentalen Entwicklung, die sich mit Begriffen wie Abstrahierung, Rationalisierung oder Formalisierung beschreiben lässt. Diese Entwicklung findet weit vor den ersten materiellen Realisierungen ihren Ausdruck in bis heute gültigen Denkmodellen wie der Turingmaschine und ihrer Programmierbarkeit. Auf dem Gebiet zeitgenössischer Kompositionstechnik gibt es Ausprägungen, die dieser Entwicklung ebenfalls entsprechen und ihr einen je spezifischen Ausdruck verleihen.
Wie schon Al-Chwarizmi sagt²⁴
Man könnte diese Technik als generatives oder programmierendes Komponieren bezeichnen. Meist wird hier aber ein Begriff verwendet, der sich tatsächlich auch im Zusammenhang der Turingmaschine findet: Algorithmus.²⁵ Ich möchte diesen Begriff an einigen Beispielen erläutern, um anschaulich zu machen, was gemeint ist.
Der Begriff des Algorithmus bezeichnet in der einfachsten Form einen Rechentrick,²⁶ durch den man einen arithmetischen Ausdruck umformen und so „lösen“ kann. Wahrscheinlich bekommen die meisten von uns ein langes Gesicht, wenn wir uns vorstellen sollen, was passiert, wenn man eine Hälfte durch drei Fünftel teilt. Aber mit dem Rechentrick geht alles wie von selbst: Man dividiert einen Bruch durch einen anderen Bruch, indem man ihn mit dem Kehrwert des zweiten multipliziert. Also:

Dieses Vorgehen lässt sich mit den Begriffen Eingabe (Input) - Transformation - Ausgabe (Output) beschreiben. Input sind die Brüche 1/2 und 3/5. Transformiert wird die Eingabe durch bestimmte beschreib- und ausführbare Vorgänge: Vertausche bei der zweiten Zahl Zähler und Nenner, dann multipliziere die beiden Zähler und Nenner miteinander. Als Ergebnis dieses „Algorithmus“ erhalte ich dann eine Ausgabe, die mir entweder als solche genügt, oder die Grundlage für den nächsten Transformationsprozess bildet.
Von einer anderen Perspektive aus gesprochen: Wenn ich einen Vorgang so beschreiben kann, kann ich ihn auch programmieren. Die Programmierung, das Schreiben eines Programms ist dann die konkrete „Implementierung“ des Algorithmus. Das kann in verschiedenen Sprachen geschehen. Ein Beispiel, in dem der obige Algorithmus als Funktion in der Programmiersprache Python definiert wird:²⁷
def teilen((zaehler1, nenner1), (zaehler2, nenner2)):
zaehler = zaehler1 * nenner2
nenner = nenner1 * zaehler2
print '%d/%d' % (zaehler,nenner)
Diese Funktion kann ich dann mit zwei Zahlen aufrufen und erhalte das Ergebnis:
teilen((1, 2), (3, 5))
-> 5/6
Ein weiteres Beispiel, mit dem der griechische Mathematiker Euklid den größten gemeinsamen Teiler zweier Zahlen bestimmt.²⁸
EINGABE
Zwei (natürliche) Zahlen
TRANSFORMATION
Ziehe die kleinere von der größeren Zahl ab. Wenn das Ergebnis Null ist, ist der größte gemeinsame Teiler gefunden.
Wenn nicht, wiederhole den Vorgang mit dem Ergebnis und der vorigen kleineren Zahl.
AUSGABE
Größter gemeinsamer Teiler.
Ausführung mit der Hand am Beispiel der Zahlen 21 und 6:
21 - 6 = 15
15 - 6 = 9
9 - 6 = 3
6 - 3 = 3
3 - 3 = 0
Ergebnis: Der größte gemeinsame Teiler von 21 und 6 ist 3.
Bei der Ausführung in einem Computerprogramm muss berücksichtigt werden, dass ich bei meinen Subtraktionen oben immer die größere Zahl zuerst gesetzt habe, „weil ich ja gesehen habe“, dass es die größere ist. Der Computer sieht es aber nicht, und so muss ich immer zuerst untersuchen, welche der beiden Zahlen die größere ist. Dies ist eine mögliche Implementierung:
def euklid(zahl1, zahl2):
# welches ist die groessere zahl
if zahl1 > zahl2:
groessere = zahl1
kleinere = zahl2
else:
kleinere = zahl1
groessere = zahl2
# differenz berechnen
diff = groessere - kleinere
# ergebnis herausgeben wenn differenz null
if diff == 0: print kleinere
# sonst weiter mit differenz und kleinerem
else: euklid(diff, kleinere)
euklid(21,6)
-> 3
Das ist ein einfaches Beispiel für die so genannte Rekursion: Eine Funktion ruft sich selbst auf, bis eine Abbruchbedingung erfüllt ist. Diese Rekursion ist hier praktisch, denn man weiss ja nicht vorher, wie viele Schritte gebraucht werden, um das Ergebnis zu ermitteln.²⁹
Nun noch ein ganz anderes Beispiel für einen Algorithmus:
EINGABE
1 Ei
75 ml Milch
1 EL Zimt
1 TL Vanillearoma
1 Prise Salz
4 Scheiben helles Brot
TRANSFORMATION
1. Ei, Milch, Zimt, Vanillearoma und Salz verschlagen. Eine leicht gefettete Brat- oder gusseiserne Pfanne bei mittlerer Hitze erwärmen.
2. Die Brotscheiben von jeder Seite in die Eiermischung legen und 20 Sekunden die Flüssigkeit aufsaugen lassen.
3. Brotscheiben in der Pfanne von beiden Seiten goldbraun und knusprig braten. Arme Ritter schmecken am besten heiß!
AUSGABE
...
Mit anderen Worten: Ein Algorithmus kann sehr lecker sein. Wer einwendet, dass dasselbe Kochrezept bei zwei Köchen zu unterschiedlichen Ergebnissen führt, hat natürlich recht. Bevor ich aber auf die verschiedenen Abweichungen oder „Zufälle“, die in einem Algorithmus stecken können, näher eingehe, möchte ich das Kochrezept untersuchen, dem Stockhausen in seiner elektronischen Studie II folgt.
Das Eine in Allem: Studie II als Programm
Es gibt wohl wenige Stücke elektronischer Musik, die besser analysiert sind und lieber besprochen werden als Stockhausens Studie II (1954).³⁰ ³¹ Das hat seinen Grund im paradigmatischen - eben studienhaften - Vorgehen einer seriellen Kompositionsweise. Im Unterschied zur Komposition für Instrumente kann Stockhausen bei diesem rein elektronischen Stück auch die Klänge selbst aus den Reihen entwickeln. Es ist also hier so etwas wie eine serielle Totalität möglich.³²
Vom Standpunkt des Programmierens aus: Umso besser! Es müsste also möglich sein, ein Programm zu schreiben, das aus einem Input alles, das ganze Stück erzeugt. Und in der Tat ist das möglich,³³ und es ist umso faszinierender, als der Input nur aus fünf Zahlen besteht: der Reihe 3 - 5 - 1 - 4 - 2.
In der Übersicht sieht es also so aus:
EINGABE
3 5 1 4 2
TRANSFORMATION
verschiedenste Verfahren, siehe unten
AUSGABE
das Stück mit seinen 380 Klängen
Um nochmal auf den Begriff des Algorithmus zurückzukommen: Es ist gleich, ob man diese Generierung in einer gesprochenen Sprache formuliert, oder in einer Programmiersprache.³⁴ Es geht nur um eine Handlungsanweisung, die ausgeführt werden kann und bei der Ausführung zu einem definierten Ergebnis führt.
Studie II lässt sich also auch als Text formulieren, der beschreibt, was man zu tun hat, um von den fünf Zahlen zu den Tonhöhen, den Lautstärken, den Dauern, den Rhythmen zu kommen. Das wird ziemlich lang,³⁵ und mag nicht unbedingt seinen Platz in den Bestsellerlisten finden.³⁶ Hier zur Illustration nur einige Auszüge aus diesem Text, gefolgt von einer Version in Programmiersprache.³⁷ ³⁸
Beispiel 1. Die Generierung des ersten „Zahlenquadrats“, also vier weiterer Reihen aus der ersten Eingabe, geht so vor sich:³⁹
EINGABE
3 5 1 4 2
TRANSFORMATION
Entwickele aus dieser Zeile vier weitere Zeilen, indem du die zweite Zeile mit der zweiten Zahl (5) beginnen lässt, die dritte mit der dritten, usw; die übrigen Zahlen einer Zeile ergeben sich dann als Transposition der „Intervalle“ der ersten Zeile.
AUSGABE
3 5 1 4 2
5 2 3 1 4
1 3 4 2 5
4 1 2 5 3
2 4 5 3 1
Eine Möglichkeit der Programmierung:⁴⁰
# hilfsfunktion zum addieren von 1 bis mod
def addmod(zahl1, zahl2, mod):
return (zahl1 + zahl2 - 1) % mod + 1
# hilfsfunktion zur ausgabe einer matrix
def printMatr(matrix):
for zeile in matrix:
for element in zeile:
print element,
print '\n',
# eigentliche berechnung
reihe = [3, 5, 1, 4, 2]
# erste zeile ist kopie der reihe
quadrat = [reihe]
# fuer alle anderen zeilen
for zeile in range(1, len(reihe)):
# transpositionsintervall ermitteln
intervall = reihe[zeile] - reihe[0]
# neue reihe schreiben
reiheNeu = [addmod(wertNeu, intervall, len(reihe)) for wertNeu in reihe]
# ans ergebnis anhaengen
quadrat.append(reiheNeu)
# als quadrat (matrix) ausgeben
printMatr(quadrat)
-> 3 5 1 4 2
5 2 3 1 4
1 3 4 2 5
4 1 2 5 3
2 4 5 3 1
Beispiel 2. Um die in dem Stück überhaupt vorkommenden Frequenzen zu bestimmen, werden, beginnend bei 100 Hz, 81 Frequenzen im Abstand ²⁵√5 zueinander ermittelt:⁴¹
EINGABE
100 Hz als Basisfrequenz, ²⁵√5 bzw 5^1/25 als Faktor
MODIFIKATION
Die Grundfrequenz mit den Faktoren 5^n/25 für n = 0, 1, 2, ... 81 multiplizieren.
AUSGABE
Eine Liste mit den 81 Frequenzen (auf ganze Hertz gerundet).
Der Code umfasst hier nur eine Zeile:
Alle_Frequenzen = [int(round(100*5**(n/25.))) for n in range(81)]
print Alle_Frequenzen
-> [100, 107, 114, 121, 129, 138, 147, 157, 167, 178, 190, 203, 217, 231, 246, 263, 280, 299, 319, 340, 362, 386, 412, 440, 469, 500, 533, 569, 607, 647, 690, 736, 785, 837, 892, 952, 1015, 1083, 1155, 1231, 1313, 1401, 1494, 1593, 1699, 1812, 1932, 2061, 2198, 2344, 2500, 2666, 2844, 3033, 3234, 3449, 3679, 3923, 4184, 4462, 4759, 5076, 5413, 5773, 6157, 6566, 7003, 7469, 7965, 8495, 9060, 9662, 10305, 10990, 11721, 12500, 13331, 14218, 15163, 16171, 17247]
Beispiel 3. Ein konkreter Klang („Tongemisch“)⁴² besteht aus fünf Frequenzen. Für ihre Ermittlung braucht man drei Zahlen. Also:
EINGABE
Drei Zahlen zur Festlegung der Gruppe (G), der Spalte (S) und der Position (P). Beispiel: G = 5, S = 5, P = 3
TRANSFORMATION
Durch G komme ich auf den Basiston einer Gruppe, indem ich in der Frequenzliste für jede Gruppe fünf Frequenzen höher gehe. Gruppe 1 steht also auf 100 Hz, Gruppe 2 steht auf 138 Hz, Gruppe 5 (das Beispiel) steht auf 362 Hz.
Durch S wird angegeben, wie groß die Abstände zwischen den einzelnen Teiltönen des Tongemischs sind: 1 = jede aufeinanderfolgende Frequenz, 2 = jede zweite, ..., 5 = jede fünfte Frequenz der Basisliste („Alle_Frequenzen“) wird benutzt. Im Beispiel sind also die Frequenzen 362, 500, 690, usw. möglich.
Durch P wird angegeben, auf welcher dieser (durch S ermittelten) möglichen Frequenzen dieser Klang tatsächlich steht: 1 = auf dem ersten, 2 = auf dem zweiten, usw. Im Beispiel mit P = 3 steht also der Klang auf der Frequenz 690 Hz.
Von dieser Frequenz aus werden nun 4 weitere Frequenzen ermittelt; in dem Abstand, den S gesetzt hatte. Zusätzlich zu 690 Hz treten also die Frequenzen 952, 1313, 1812 und 2500 Hz.
AUSGABE
Ein „Tongemisch“ aus 5 Frequenzen.
Der Code ist wiederum erheblich kürzer⁴³ und macht sich zunutze, dass es eigentlich nur um das Aufsuchen von Positionen innerhalb der Liste aller möglichen Frequenzen geht:
# Input
G = 5
S = 5
P = 3
# Index (in Alle_Frequenzen) für die Basisfrequenz der Gruppe bestimmen
Index_G = (G-1)*5
# Index für die tiefste Frequenz der Mischung ermitteln
Index_P = Index_G + (P-1)*S
# die Liste herausgeben
Tongemisch = [Alle_Frequenzen[Index_P + n*S] for n in range(5)]
print Tongemisch
-> [690, 952, 1313, 1812, 2500]

Stockhausen Studie II Tonhöhen und Klanggruppen (Silberhorn S. 17, vgl. Partitur S. V)
Die Zahlen G, S und P kommen nun aus verschiedenen Reihen.⁴⁴ Der Ablauf dieser Reihen (in je verschiedenen Geschwindigkeiten) erzeugt somit „geradeheraus“ die Tongemische in den verschiedenen Teilen. Die folgende Abbildung zeigt das für den Anfang:⁴⁵
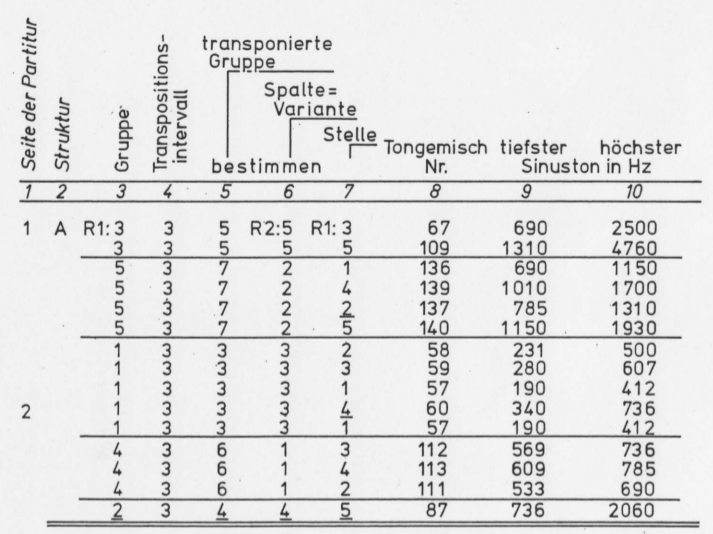
Stockhausen Studie II Reihenablauf für die Tonhöhen am Anfang (Silberhorn S.128)
Ich hoffe, es ist ein Eindruck davon entstanden, wie man Studie II als Programm verstehen und in einer geläufigen Programmiersprache generieren kann. Tut man das, gerät man allerdings auch auf Ereignisse, die dem Programmierer zu schaffen machen, und die deshalb für mein Thema besonders interessant sind. Dazu später mehr.
Immer anders kochen: Williams Mix
Als es vorhin um das Kochrezept als Beispiel für einen Algorithmus ging, tauchte die Frage auf, warum ein und dasselbe Rezept bei verschiedenen Köch(inn)en verschieden schmeckt. Die wissenschaftlich-trockene Antwort ist einfach: Der eine nimmt eben etwas mehr Salz, die andere lässt die armen Ritter schärfer schmoren. Die Ausführung des Algorithmus ist also nicht gleich, und wäre sie es, wären auch die Ergebnisse gleich wohlschmeckend, fade oder versalzen.
Das mag wohl sein, doch führt die Beobachtung von Abweichungen zu einem gänzlich anderen Typ von Algorithmus als dem bei Stockhausen (bzw. in der seriellen Musik) zu studierenden. Es gibt nämlich Algorithmen, in die Abweichungen mit eingeschrieben sind. Das können zufällige Abweichungen sein, oder auch Entscheidungen, die den Ausführenden überlassen werden.⁴⁶ Zu beiden Begriffen - dem Zufall und der Entscheidung - lohnt sich eine kleine Abschweifung.
Zufall. Immer wieder hört man, wenn es auf das Thema Zufall kommt, etwas wie: „Ah, Zufall - dann ist ja alles egal!“ Das ist aus mehreren Gründen sehr oberflächlich: (a) Zufall findet nur in einem bestimmten Rahmen statt, (b) Zufall findet in einer bestimmten Verteilung statt, (c) Zufall findet in einer bestimmten Skalierung statt. Nehmen wir als Beispiel eine „zufällige Tonhöhe“:
(a) Was sind die Grenzen? Eine Anzahl zufälliger Tonhöhen zwischen 20 Hz und 10000 Hz wird sich ziemlich anders anhören als eine Anzahl zufälliger Tonhöhen zwischen 1000 Hz und 1001 Hz.
(b) Angenommen ich habe zufällige Tonhöhen zwischen 100 und 800 Hz. Dann ist die Frage, wie sich diese Tonhöhen auf den Bereich verteilen: Gleichverteilt, so wie bei vielen Münzwürfen etwa gleich oft „Kopf“ und „Zahl“ kommt?⁴⁷ Oder in irgendeiner ungleichen Verteilung, wie sie in der Natur oft anzutreffen sind?⁴⁸
(c) Wenn ich die bei (b) ermittelten Tonhöhen von einem Klavier spielen lasse, werden sie „von selbst“ auf die gleichschwebende chromatische Stimmung skaliert. In der Elektronik bin ich normalerweise frei, die Skalierung selbst zu bestimmen.⁴⁹
In aller Regel werden die Grenzen, die Verteilung und die Skalierung (also alles vorgenommene Setzungen und keine „Zufälle“) das klangliche Ergebnis viel stärker bestimmen als die konkrete Ausprägung des Zufalls.
Entscheidung. Entscheidung klingt nach dem, was man vielleicht als Gegenstück einer algorithmischen Anweisung assoziieren mag: Freiheit. Aber zumindest sollte man sich klar machen, dass es auf die Art der Entscheidung ankommt, die jemandem angeboten wird. Wenn ich zwischen zwei Klängen wählen kann, kann das eine wichtige Entscheidung sein (wenn beispielsweise die Klänge sehr verschieden sind); es kann aber auch belanglos sein. Zu anderen Aspekten von Entscheidung komme ich später noch.
Cage hat in Williams Mix eine Konzeption geschaffen, die auf verschiedenen Ebenen immer wieder neu realisiert werden kann. Jedesmal entsteht ein neues Williams Mix - unter Umständen sehr verschieden von dem Cageschen, aber doch programmierbar, und doch eine Erfüllung seiner Konzeption. Beginnen wir mit einem Blick auf die Partitur, um die ersten Ebene des „immer neu“ zu diskutieren.

Cage Williams Mix Partitur S. 5 (Kostelanetz, Cage, S. 158)
Jede Partiturseite besteht aus zwei Akkoladen. Jede Akkolade enthält eine maßstabsgetreue⁵⁰ Abbildung der acht einzelnen Tonbänder.⁵¹ Nun sieht man auf jedem der einzelnen Schnipsel eine Folge von einem großen und drei kleinen Buchstaben. Die Großbuchstaben beziehen sich auf die sechs Kategorien, in die Cage die Klänge einteilt:⁵²
A) Stadtklänge
B) Landklänge
C) Elektronische Klänge
D) Manuell produzierte Klänge einschließlich solcher der Musikliteratur
E) Mit Atem erzeugte Klänge einschließlich der Lieder
F) Leise Klänge, die elektrisch verstärkt werden müssen, damit man sie zusammen mit den anderen hören kann
Sehen wir also rechts unten einen Schnipsel mit der Bezeichnung Dvvc, stammt dieser aus der Gruppe manuell produzierter Klänge, also beispielsweise ein Ausschnitt aus einer Beethovensonate, oder das Klopfen an der Tür. Drei Spuren darüber steht Cccv und unmittelbar darüber Ccvc; beide Klänge stammen also aus der Kategorie der elektronischen Klänge.
Die kleinen Buchstaben geben nun an, ob ein solcher Klang bearbeitet (c = controlled) oder unbearbeitet (v = variable) auftreten soll, und zwar in den Parametern Tonhöhe, Klangfarbe und Lautstärke. Der Unterschied zwischen den Klängen Cccv und Ccvc besteht also darin, dass Cccv in der Lautstärke verändert wurde, während bei Ccvc in die Klangfarbe eingegriffen wurde (beispielsweise durch Filter).
Die erste Ebene von Veränderung besteht also darin, auf Basis der gegebenen Vorschrift⁵³
* andere Klänge („Samples“) einzusetzen, und/oder
* andere Modifikationen vorzunehmen.⁵⁴
Diese erste Ebene ergibt schon eine enorme Breite an möglicher Veränderung.⁵⁵ Cage hat das bewusst freigelassen: „Das ist eine sehr freie Art, die Herstellung zu ermöglichen, und ich lasse den Ingenieuren, die die Klänge machen, völlig freie Hand. Ich gebe ihnen einfach eine Liste mit den Klängen, die ich brauche, z.B. EvcvFvvv (zweifache Klangquelle).“⁵⁶
Kann man diese Veränderungen programmieren? Ja, gewiss; nur dass das Programm gewisse Zufallsanteile (random choices) aufweist. Die Struktur wäre so:
* Es gibt eine Datenbank mit sechs Gruppen von Klängen.
* Es gibt eine Sammlung definierter Veränderungen der Tonhöhe,⁵⁷ der Klangfarbe⁵⁸ und der Lautstärke.
Bekommt das Programm nun an einer Stelle die Anweisung Dvvc, so sucht es zunächst aus der Gruppe D einen Klang, ermittelt die Stelle, von wo er abgespielt werden soll, und verändert schließlich dessen Lautstärke. Um einen Eindruck zu geben, wie ein Code aussehen könnte, der einen zufälligen Klang aus einer Gruppe aussucht:
D = ["beethoven.wav", "tuer.wav", "trommel.wav", "hey_joe.wav", "jazz.wav"]
from random import randint
Zufallsauswahl = D[randint(0,4)]
print Zufallsauswahl
-> trommel.wav (beim ersten Mal)
-> jazz.wav (beim zweiten Mal)
Die zweite Ebene von Veränderung betrifft das, was wir als Partitur vorfinden. Das sind nicht nur die Buchstaben für die Klänge und deren Modifikationen. Es ist auch das gesamte „Schnittmuster“, also die Dauer eines Klanges und dessen Ein- und Ausblende. All diese Bestimmungen, die dann konkret gefüllt bzw. ausgeführt werden können, sind generiert worden. Cage arbeitet dazu mit Kärtchen und Tabellen, die nach einem ziemlich komplizierten Verfahren mit Hilfe von Münzwürfen zu allen („zufälligen“) Festlegungen führen.⁵⁹
Mit anderen Worten: Man könnte aus ebendiesen Tabellen und Kärtchen viele andere Partituren von Williams Mix erzeugen - sei es per Hand oder mit Hilfe eines Computerprogramms. Man würde also Partiturvarianten generieren, die strukturell untereinander ganz ähnlich sind, aber doch immer andere Zusammensetzungen im Einzelnen aufweisen.
Und schließlich die dritte Ebene: Die Tabellen und die Art, wie mit ihnen umgegangen wird, beruht auf kompositorischen Grundentscheidungen, beispielsweise über die mögliche Dichte von Ereignissen. Hier ließen sich andere Entscheidungen treffen; ganz ähnlich zu den verschiedenen Arten, wie Stockhausen in Studie II die Reihenabläufe liest.
Insgesamt gibt es also in Williams Mix drei Ebenen, deren jede unendlich viele Variationsmöglichkeiten aufweist.⁶⁰ Jede Realisierung ist eine Auswahl aus einer Anzahl von Möglichkeiten.

Die Auswahl kann entweder von Menschen mit teils „freien“ („diesen Klang will ich jetzt nehmen“), teils „zufälligen“ (drei Münzen werfen) Entscheidungen vorgenommen werden, oder von einem Computerprogramm. Strukturell ist das kein Unterschied.
Wo bleibt da die Kunst
Wenn dem so ist, und man sowohl Studie II als auch Williams Mix als Computerprogramm realisieren kann:⁶¹ was unterscheidet dann beide Stücke von einer mathematischen Formel? Was ist das spezifisch Künstlerische an diesem „algorithmischen“ kompositorischen Denken, und welche Qualitäten, welche Unterschiede gibt es innerhalb dieser Art zu komponieren?
Verrücktheit. Schon die sechs Kategorien von Klängen in Williams Mix sind bei genauerem Hinsehen recht merkwürdig. Eigentlich wäre mit den ersten beiden (Stadt- und Landklänge) alles abgedeckt, was es an Klängen gibt. Abgedeckt und --- langweilig. Es geht hier nämlich nicht um eine Kategorisierung im Sinne eines wissenschaftlichen Erfassens,⁶² sondern um einen eigentümlichen Blick auf die (klingende) Wirklichkeit. Eigentümlich ist immer auch ein wenig verrückt, und Verrücktheit gehört zur Kunst. Erfrischend verrückt ist bei Cage nicht nur die Kategorisierung der Klänge, sondern auch das hyperdetaillierte Vorgehen in der Ausarbeitung, das die alte chinesische Orakeltradition „wendet“.⁶³ All dies steht einem „Denken mit dem Computer“ nicht entgegen, da der Computer ja nur „konsequent“ ausführt, was an Rahmenbedingungen gesetzt wurde.
(Selbst-) Kritisches Hören. Es ist äußerst faszinierend zu beobachten, wie Stockhausen während der Arbeit an „Studie II“ auf das reagiert, was da generiert wird, und in der Folge zu bestimmten Veränderungen des ursprünglichen Plans (Algorithmus') kommt. Das sind Veränderungen auf folgenden Ebenen:
* Die Auswahl der Tonhöhen ergeben sich bei Studie II aus insgesamt neun Gruppen, wie wir sahen.⁶⁴ Stockhausen hatte offenbar geplant, für jeden der fünf Teile fünf nebeneinander liegende Gruppen auszuwählen. Die Regel dafür ist: Eine Reihe bestimmt die Auswahl einer Gruppe (1-5), und dazu kommt für einen Teil ein konstanter „Transpositionsfaktor“.⁶⁵ Nachdem Stockhausen das in den ersten beiden Teilen mit den Transpositionen 3 und 5 durchgeführt hatte, ändert er im dritten Teil die Regel. Statt einer konstanten 1 nimmt er eine andere Reihe und lässt diese so schnell durchlaufen, dass alle neun Gruppen in diesem Teil vorkommen. - Der Grund für diese Veränderung dürfte darin liegen, dass Stockhausen für diesen „Staccato“ Teil mehr und extremere Sprünge wollte. Wäre er „stur“ bei seiner ursprünglichen Methode geblieben, hätte dieser Teil ein anderes (und blasseres) Gesicht bekommen.⁶⁶
* Grundsätzlich gilt in der gesamten Komposition, dass Stockhausen das, was ihm die Reihen erzeugen, von Teil zu Teil verschieden liest. Das betrifft vor allem die Dauern. Durch verschiedene Lesart der Einsatzabstände kommt Stockhausen beispielsweise dazu, dass Teil 3 aus kurzen Klängen besteht, während sich die Klänge in Teil 4 zu großen Schichtungen auftürmen.
* Dies alles lässt sich ohne weiteres programmieren, da es zwar die Regel ändert, aber in sich regelhaft bleibt.⁶⁷ Anders ist es dagegen im fünften Teil. Hier will Stockhausen alle bisherigen Fakturen kombinieren, und in der Arbeitspartitur finden sich am rechten Rand Bemerkungen, die darauf hindeuten, dass diese Auswahl spontan geschah.⁶⁸ Das ist sehr aufregend zu sehen, und hier findet gleichzeitig die Programmierbarkeit ihre Grenze. Diese Entscheidungen sind offensichtlich weder regelhaft noch zufällig, sondern musikalisch-intuitiv. Das kann man beim Nachprogrammieren nicht nachbilden - es sei denn man fände übergeordnete Gesetze dieser Intuition -, und der daraus entstehende Code ist eine Qual für jeden Programmierer, weil er die Ereignisse nur nachpinseln kann, anstatt sie wirklich zu generieren.⁶⁹
Das heisst: Der Algorithmus ist kein Selbstzweck, sondern er dient dazu, eine bestimmte künstlerische Idee zu verwirklichen. Die Arbeit am Algorithmus ist es, die dazu führt, dass die künstlerische Idee mehr oder weniger erreicht wird. Diese Arbeit, diese Fähigkeit zum Sich-Zuhören und Sich-Korrigieren, kann man an Studie II wunderbar studieren.
Intuition. Zu diesem Sich-selbstkritisch-Zuhören gehört ebenfalls die Frage nach der kompositorischen Intuition. Bei Cage betrifft das etwa die Frage nach der Dichte der musikalischen Faktur. Wenn man einmal die Gelegenheit hat, Williams Mix als Originalversion für 8 Lautsprecher zu hören, und dann zum Vergleich in einer Zusammenmischung auf Stereo, merkt man, was das heisst. Letzteres ist „zu dicht“; man kann hörend nicht mehr genug unterscheiden und das Ganze wird zu einer recht undurchdringlichen Wand. Das heisst umgekehrt, dass Cages Intuition für die Achtkanalversion richtig war - dort ist es „dicht genug“ um verwirrend zu sein, aber es gibt noch genug „Luft“ für Unterschiede.
Wandel der Phantasie. Es geht also auch in dieser scheinbar so automatischen Kompositionsweise um „Ideen“, und es gibt langweilige oder spannende Ideen.⁷⁰ Ich denke, dass beide hier diskutierten Stücke zu einem Typus in Neuer Musik gehören, bei dem sich die kompositorische Phantasie a) auf die Imagination des Ganzen, und b) auf die Methoden seiner Generierung richtet. Wer also nach der Phantasie sucht, sucht an falscher Stelle, wenn er auf die Ausführung der Ableitungen schaut. Die Phantasie ist da, und unverzichtbar, aber sie ist woanders hingewandert.
Algorithmische Komposition beginnt also in der elektronischen Musik längst vor der Einführung des Computers. Cage und Stockhausen „programmieren“ ihre Musik zu einer Zeit, als diese Programmierung noch nicht mit dem Computer umgesetzt werden konnte. Ihre Stücke zeigen, dass ein tiefer innerer Zusammenhang besteht zwischen dem, was sich in der Neuen Musik der 50er Jahre an Kompositionstechnik entwickelte, und dem, was sich gleichzeitig an Programmierbarkeit des Computers herausbildete. Williams Mix und Studie II zeigen gerade in ihrer Unterschiedlichkeit, worauf es ankommt, wenn algorithmische Komposition originell und zum Hören bestimmt sein soll: Die Regelhaftigkeit stets daraufhin zu befragen, ob sie dem imaginierten musikalischen Bild dient, anstatt sie zu einem Fetisch zu machen. Es scheint, dass zu einer Zeit, in der die algorithmische Komposition noch in den Kinderschuhen steckte, bei aller persönlichen Mühsal⁷¹ entscheidende künstlerische Fragestellungen schärfer gesehen und produktiver gelöst wurden, als in vielen Erzeugnissen einer Zeit, in der es leicht ist, ohne Idee eine Musik zu erzeugen, deren Algorithmen so schnell bei der Hand sind wie eine „App“.
1 Obwohl von einer Emphase des Fortschritts aus betrachtet beides zusammengehören sollte: „Die Musik hat für ihre Klangverwirklichung immer jene, in verschiedener Weise bestimmten Mittel, die aus einer bestimmten historischen Situation in der Entwicklung der technisch-strukturell-sprachlichen Möglichkeiten folgen, verwendet. Natürlich geben diese neuen Möglichkeiten den Anstoß zu neuen Konzepten. Dies geschieht auch heute, besonders im Zusammenhang mit den elektronischen Mitteln.“ (Luigi Nono, Über elektronische Musik (1961), in: Luigi Nono, Texte, Hg. Jürg Stenzl, Zürich 1975, S. 149)
2 Jedenfalls haben sich meines Wissens sowohl Cage als auch Stockhausen erst sehr viel später, und ohne selbst zu programmieren, mit dem Computer befasst.
3 http://de.wikipedia.org/wiki/ENIAC (Zugriff 13.1.2014)
4 http://en.wikipedia.org/wiki/History_of_computing_hardware (Zugriff 13.1.2014)
5 In der ersten Version nur etwa 300 Bytes (http://www.hpmuseum.org/tech9100.htm, Zugriff 13.1.2014)
6 http://de.wikipedia.org/wiki/HP-9100A (Zugriff 13.1.2014)
7 Etwa Tandy TRS-80, Apple II oder Commodore Pet 2001.
8 Wobei die Kunst und die Wissenschaft natürlich mit gesellschaftlichen, insbesondere ökonomischen Prozessen verbunden sind. Vom Standpunkt einer kritischen Soziologie aus formuliert: „Der Einsatz des Computers setzt (...) jenen historischen Wandlungsprozess voraus, der (...) ihn selbst überhaupt erst denkbar gemacht hat und der dazu geführt hat, daß sich Menschen in zunehmendem Maße 'mechanisch' zu verhalten hatten.“ (Dieser Wandlungsprozess wird in der Soziologie als Rationalisierung bezeichnet. In der Arbeitsorganisation findet er beispielsweise Ausdruck im „scientific Management“ desTaylorismus.) Bettina Heintz, Die Herrschaft der Regel, Zur Grundlagengeschichte des Computers, Frankfurt / New York 1993, S. 10.
9 Wie tief diese Krise ging, wird anekdotisch in der (öffentlichen) Wette der beiden Mathematiker Hermann Weyl und George Pólya (ETH Zürich) deutlich. Sie wetteten 1918, ob in 20 Jahren folgende Sätze noch gelten würden oder nicht:
1) Jede beschränkte Zahlmenge hat eine präzise obere Grenze.
2) Jede unendliche Zahlmenge enthält eine abzählbare Teilmenge.
(Hans Wußing, 6000 Jahre Mathematik, Berlin Heidelberg 2009, S. 458)
10 Klassisch bei Euklid: „Die Axiome beschreiben gewisse durch die Anschauung (d.h. visuelle Sinneswahrnehmung) unmittelbar gegebene Eigenschaften des Raumes, während die übrigen geometrischen Sätze dann durch rein logisches Schließen (und Anwendung der Arithmetik) ohne Verwendung der Anschauung bewiesen werden.“ (Heinz Bachmann, Der Weg der mathematischen Grundlagenforschung, Bern 1983, S. 15)
11 „Alles, was im bisherigen Sinne die Mathematik ausmacht, wird streng formalisiert, so daß die eigentliche Mathematik oder die Mathematik im engeren Sinne zu einem Bestand an Formeln wird. [...] Zu der eigentlichen, so formalisierten Mathematik kommt eine gewissermaßen neue Mathematik, eine Metamathematik, die zur Sicherung jener notwendig ist, in der - im Gegensatz zu den rein formalen Schlussweisen der eigentlichen Mathematik - das inhaltliche Schließen zur Anwendung kommt, aber lediglich zum Nachweis der Widerspruchsfreiheit der Axiome. In dieser Metamathematik wird mit den Beweisen der eigentlichen Mathematik operiert und diese letzteren bilden selbst den Gegenstand der inhaltlichen Untersuchung.“ (Hilbert 1922, zitiert nach: Wußig (Anm. 8), S. 459)
12 dass sich also alle Aussagen in ihm aus ihm ableiten lassen - sonst wäre ja wieder der Außenbezug gegeben
13 In der Formulierung von Hans Magnus Enzensbergers Hommage à Gödel (H. M. Enzensberger, Die Elixiere der Wissenschaft, Frankfurt 2002, S. 9)
14 Vgl. Bachmann (Anm. 9), S. 212
15 Beim Gödelisieren werden die einzelnen Zeichen einer formalen Sprache durchgezählt. Eine Verbindung solcher Zeichen (beispielsweise in einer Formel oder Aussage) wird dann dargestelt, indem fortlaufende Primzahlen die Indices als Exponent bekommen und das Produkt aus diesen gebildet wird. Wenn z.B. die Sprache nur aus den Elementen {1, 2, 3, +, =} besteht, dann würde der Satz "1 + 2 = 3" in dieser Gödelisierung lauten: 2¹·3⁴·5²·7⁵·11³ = 90598973850 (das Verfahren nach http://de.wikipedia.org/wiki/Gödelisierung (Zugriff 17.1.2014); ein anderes Verfahren bei Bachmann (Anm. 9), S. 198f).
16 Der von Turing deutsch zitierte Ausdruck bezieht sich auf die Frage der Entscheidbarkeit in der Formulierung von Hilbert und Ackermann aus dem Jahre 1931 (Alan Turing: On Computable Numbers, with an Application to the Entscheidungsproblem. In: Proceedings of the London Mathematical Society. Bd. 42, 1937, S. 259). Es geht um die Frage, ob es ein Verfahren gibt, das entscheidet, ob eine Formel auf ein Theorem der Prädikatenlogik zurückgeführt werden kann oder nicht. Vgl. Bachmann (Anm. 9) S. 207, oder auch http://de.wikipedia.org/wiki/Entscheidungsproblem.
17 „Computing is normally done by writing certain symbols on paper. We may suppose this paper is divided into squares like a child's arithmetic book. In elementary arithmetic the two-dimensional character of the paper is sometimes used. But such a use is always avoidable, and I think that it will be agreed that the two-dimensional character of paper is no essential of computation. I assume then that the computation is carried out on one-dimensional paper, i.e. on a tape divided into squares. “ (Turing (Anm. 15), S. 249)
18 Eine gute Darstellung der Funktionsweise findet sich bei Bachmann (Anm. 9), S. 201-203.
19 indem bewiesen wird, dass es nicht lösbar ist
20 Alonzo Church, An Unsolvable Problem of Elementary Number Theory. In: American Journal of Mathematics, Vol. 58, No. 2 (1936), S. 345-363 (auch auf http://www.jstor.org/stable/2371045)
21 „As a corollary (..), it follows that the Entscheidungsproblem is unsolvable in the case of any system of symbolic logic which is ω-consistent (ω-widerspruchsfrei) (...) and is strong enough to allow certain comparatively simple methods of deifinition and proof.“ (Church (Anm. 19), S. 363)
22 Vor allem von Lisp (zuerst 1958), das den Lambda-Kalkül in Ausdrücken wie ((lambda (x) (x+2)) 3) direkt ausdrückbar macht. Von hier aus ist er in viele andere Programmiersprachen gewandert. Lisp ist auch als „(selbst-)programmierbare Programmiersprache“ paradigmatisch: Programm und Daten haben dieselbe Struktur, so dass ein Programm ein anderes Programm selbst erzeugen kann.
23 Claude Shannon, A Symbolic Analysis of Relay and Switching Circuits. In: Transactions of the American Institute of Electrical Engineers, Vol. 57, Issue 12 (1938), S. 714
24 Der iranische Mathematiker schrieb um 825 sein „Buch über das Rechnen mit indischen Ziffern“. Durch - freundlich ausgedrückt - Latinisierung wurde sein Name im Mittelalter in Formen wie Algorismi, Algoritmi und ähnlichem überliefert. (Die älteste lateinische Übersetzung beginnt mit „DIXIT algorizmi“ - Abbildung auf http://upload.wikimedia.org/wikipedia/commons/4/43/Dixit_algorizmi.png.) Ein „Algorithmus“ ist also vom Wortsinn her „etwas, das Al-Chwarizmi“ macht, also als Methode beschreibt (vor allem in seinem „Buch über die Rechenverfahren durch Ergänzen und Ausgleichen“). Vergleiche auch: Menso Folkerts, Die älteste lateinische Schrift über das indische Rechnen nach al-Hwarizmi, München 1997, sowie Kurt Vogel, Mohammed ibn Musa Alchwarizmi's Algorismus, Aalen 1963
25 bzw. „algorithmische Komposition“, beispielsweise in Martin Supper, Elektroakustische Musik und Computermusik, Hofheim 1997, S. 63 u.ö.
26 Oder neutraler gesagt: eine Vorgehensweise. Ich beziehe mich hier mehr auf das umgangssprachliche „frei nach Adam Riese“ (dessen 1518 verfasstes Rechnung auf der Linie „über weite Strecken nichts anderes ist als eine 'Übersetzung' von Al-Khowarizmis Buch“ ist (U.Schöning, Ideen der Informatik, München 2006, S. 3)). Eine mathematische Definition lautet: „Wenn endlich viele eindeutige Regeln oder Anweisungen gegeben sind, wobei man nach Anwendung einer Regel nicht eine beliebige weitere Regel anwenden darf (wie dies in einem Kalkül gestattet ist), sondern nach jeder Regel stets eine ganz bestimmte weitere Regel anwenden muss, so spricht man von einem Algorithmus.“ (Bachmann S. 196)
27 Zur Erklärung der folgenden vier Zeilen:
(1) Eine Funktion namens „teilen“ wird definiert. Sie erwartet zwei Zahlen in der Schreibweise (Zähler, Nenner) als „Argumente“.
(2)(3) Zähler und Nenner des Ergebnisses werden nach der besprochenen Rechenregel bestimmt.
(4) Das Ergebnis wird herausgegeben. Das sieht hier etwas umständlicher aus als es ist: %d sagt nur, dass eine ganze Zahl erwartet wird. Der Ausdruck '%d/%d' ist also die allgemeine Formulierung dessen, dass ich das Ergebnis in einer Form sehen möchte, in der zwei Zahlen durch einen Schrägstrich voneinander getrennt sind. Rechts des „%“ Zeichens steht dann das, was in diesen allgemeinen Ausdruck eingesetzt wird, also Zähler und Nenner des Ergebnisses.
Zu Python siehe www.python.org. Ich verwende Python 2.7.
28 Oder in der damals noch selbstverständlichen Anschaulichkeit: Was ist die größtmögliche Maßeinheit, mit der man zwei Strecken abzählen kann. (Vgl. die Darstellung auf http://de.wikipedia.org/wiki/Euklidischer_Algorithmus (Zugriff 8.1.14).)
29 Zu jeder rekursiven gibt es eine iterative Lösung. In diesem Fall, in dem Code von Wolfgang Fohl:
def euklidi(groessere, kleinere):
while kleinere > 0:
if groessere < kleinere: (kleinere, groessere) = (groessere, kleinere)
diff = groessere - kleinere
(kleinere, groessere) = (diff, kleinere)
print groessere
30 Partitur (nachträglich geschrieben): Karlheinz Stockhausen, Nr. 3 Elektronische Studien, Studie II, London (Universal Edition 12466) 1956. Tonband (1954, Mono) beispielsweise auf CD 3 der Complete Edition (Stockhausen-Verlag).
31 Erst kürzlich widmete die italienische Zeitschrift le arti del suono (no. 6) der Studie II noch einmal einen Themenschwerpunkt.
32 Und an Totalität war Stockhausen bekanntlich auch sonst sehr interessiert.
33 Siehe unten für die umso spannenderen Einschränkungen.
34 Ebenso ist es gleich, ob man das regelhafte Vorgehen selbst beschreibt oder nicht. Um die Regelhaftigkeit und ihre Reproduzierbarkeit geht es.
35 Die Analyse von Heinz Silberhorn, der ich weitgehend folge, umfasst 167 Seiten (Heinz Silberhorn, Die Reihentechnik in Stockhausens Studie II, Rohrdorfer Musikverlag 1980).
36 Auch der mit „Es waren einmal fünf Zahlen“ beginnenden Märchenversion dürfte im Zeitalter des durch die elektronischen Medien veränderten Freizeitverhaltens (lange Winternächte werden generationenübergreifend vor Internet-Streaming-Angeboten verbracht) kein durchschlagender Erfolg beschieden sein.
37 Wie wohl jede und jeder Programmierende bestätigen kann, ist das „Schreiben“ solch eines Textes (der dann vielleicht als Kommentar erscheint) die Hauptarbeit des Programmierens. Wenn das, was man tun will, klar ist, ist das Codieren nur noch eine Formsache.
38 Eine vollständige Re-Generierung habe ich in der Audio-Programmiersprache Csound unternommen, was den Vorteil hat, dass man das Ergebnis der Generierung auch hören kann (in einer vereinfachten Version mit Sinustönen, wie in Georg Hajdus Version für die Programmiersprache Max).
Code: http://joachimheintz.de/soft/Stockhausen-Studie_II_dt.csd
Beschreibung: Joachim Heintz, Re-Generating Stockhausen's Studie II in Csound, in: Proceedings of the Linux Audio Conference 2010, Utrecht 2010, S. 65-73 (http://lac.linuxaudio.org/2010/papers/34.pdf)
39 Der im folgenden gebrauchte Begriff des Intervalls kann mit einer Pentatonik verglichen werden, bei der die Töne von 1 bis 5 nummeriert werden. Das Intervall 3 - 5 heisst: zwei Töne höher. Beginnend mit der 1 (statt der 3) ergibt sich 1 - 3. Beginnend mit der 2 ergibt sich 2 - 4. Beginnend mit der 4 ergibt sich 4 - 1 (weil „oben nach der 5“ wieder die 1 erscheint). Und beginnend mit der 5 ergibt sich 5 - 2.
40 Herzlichen Dank an dieser Stelle an Wolfgang Fohl, Hamburg, für die vielen Verbesserungen in den Code-Beispielen.
41 ²⁵√5 entspricht einem Abstand, der etwas (11,5 Cent) größer ist als der gleichschwebend temperierte Halbton.
42 Stockhausen im Vorwort zur Partitur (Anm. 31), S. IV
43 Es ginge sogar als Einzeiler:
Tongemisch = [Alle_Frequenzen[(G-1)*5 + (P-1)*S + n*S] for n in range(5)]
44 Zwei Reihen sind nötig, um G zu bestimmen. Beide Reihen bestehen wie immer aus den Zahlen 1-5, aber die zweite Reihe „transponiert“ die erste. So wird aus 3-5-1-4-2 und bei einer Transposition von 3 die Folge 5-7-3-6-4 (und so können alle neun Gruppen erreicht werden).
45 Silberhorn S. 128 („Stelle“ bezeichnet das, was ich oben „Position“ genannt habe).
46 Von letzerem kann man wohl vorläufig nur reden, wenn Menschen den Algorithmus ausführen (und kein Computerprogramm). Dem Algorithmus sollte das egal sein; er lässt an einer bestimmten Stelle nur offen, dass es nach links oder rechts gehen kann, ohne sich für die Gründe dieser Entscheidung „weiter zu interessieren“.
47 In diesem Fall ist noch zu berücksichtigen, dass eine zahlenmäßige Gleichverteilung keine Gleichverteilung für das Ohr ist: Zwischen 100 Hz und 800 Hz liegen drei Oktaven; bei einer numerischen Gleichverteilung würde aber die höchste Oktave (400-800 Hz) viel häufiger erscheinen als die niedrigste (100-200 Hz).
48 Eine Übersicht über die gebräuchlichsten Verteilung findet sich unter anderem in Charles Dodge & Thomas A. Jerse, Computer Music, New York 1985, S. 266-278.
49 Und keine Skalierung ist auch eine Skalierung, und wahrscheinlich das Verschenken einer Möglichkeit.
50 Es handelt sich quasi um ein Schnittmuster im Verhältnis 1:1; eine Partiturseite entspricht einer Dauer von 1,3 Sekunden.
51 So weit ich weiss, handelt es sich um das erste Stück für acht Lautsprecher überhaupt. „Wir haben das Stück an der Universität von Illinois [am 22.3.1953] mit 8 Tonbandgeräten und 8 Lautsprechern aufgeführt. Die 8 Geräte standen gut sichtbar auf der Bühne, die 8 Lautsprecher waren um das Publikum herum (etwa 800 Leute) aufgestellt. (...) Diese 8 Lautsprecher zu hören ist eine außergewöhniche Erfahrung. Nichts hat Platz, außer dem unmittelbaren Zuhören. Die Luft war so belebt, dass man ein Teil davon wurde.“ Cage in einem Brief an Boulez vom 1. Mai 1953 (Pierre Boulez und John Cage, Der Briefwechsel, Hg. J.-J. Nattiez, Hamburg 1997, S. 159)
52 John Cage, Williams Mix, in: Richard Kostelanetz, John Cage, Köln 1973, S. 159
53 Beispielsweise „nimm einen Klang aus der Gruppe C und verändere seine Klangfarbe“
54 So kann ja eine Veränderung der Lautstärke sowohl „lauter“ als auch „leiser“ heissen (und in welchem Maß), und beim Einsatz eines Filters kommt man natürlich zu ganz unterschiedlichen Ergebnissen, je nachdem, ob man einen Hoch-, Tief- oder Bandpassfilter einsetzt (und wiederum: mit welchen konkreten Einstellungen).
55 Man stelle sich nur einmal einen Extremfall vor, in dem es nur je einen Klang in den Kategorien A-F gibt.
56 Cage in einem Brief an Boulez, Sommer 1952 (Briefwechsel (Anm. 49), S. 146). Das ist sicher eine sympathische, aber für das klangliche Ergebnis nicht unproblematische Haltung. Beispielsweise hört man in Williams Mix dass es in der Kategorie B (Landklänge) vor allem eine Aufnahme gibt: ein Froschquaken. Dadurch wird dieser Klang manchmal etwas penetrant.
57 im einfachsten Fall beispielsweise Transpositionen zwischen plus/minus einer Oktave
58 beispielsweise zunächste die Auswahl zwischen Filtern oder Verhallen, und dann die Auswahl des Wie bzw. Wieviel
59 „Drei Münzen ergeben sechsmal geworfen eine oder zwei Ziffern von 1 bis 64. Es wurden getrennte Tabellen angelegt, die jeweils 64 Elemente aufwiesen: eine für die rhythmische Struktur (11 mal 46, dividiert durch 5, 6, 16, 3, 11, 5), eine andere, um die Faktoren zu bestimmen, welche die Strukturteile verkürzen oder verlängern, 16 für Klänge und Stillen, 16 für Dauern, 16 für die Ein- und Ausschwingvorgänge der Klänge. Eine andere Tabelle bestimmte, wie viele von den 16 innerhalb einer gegebenen Teilstruktur einzusetzen waren. Da nur 8 Spuren vorhanden waren, erbrachte die gleichzeitige Aktivierung von acht Tabellen eine maximale Dichte, die von 16 dagegen eine maximale Zersplitterung. Zu Beginn jeder der 11 Struktureinheiten wurde festgesetzt, welche der 16 (gerad- oder ungeradzahligen) Tabellen beweglich und welche unbeweglich sein sollte. Wenn eine Tabelle beweglich war, verschwand das einmal benutzte Element und ließ ein neues hervortreten; war sie unbeweglich und wurde sie benutzt, konnte dasselbe Element erneut benutzt werden. Ersatz für benutzte Elemente der beweglichen Tabellen bot ein Stapel spezieller Karten (einen Klang, eine Dauer, ein Einschwing- oder Ausschwing-Muster verzeichnend. die ebenso mittels Permutation der Möglichkeiten zustande gekommen, aber nicht zuvor in die Tabellen aufgenommen worden waren).“ John Cage, Williams Mix, in: Kostelanetz (Anm. 50), S. 159f
60 Diese Denkweise hat Cage dann in den Variations programmatisch fortgesetzt.
61 Diese Realisierung würde bei Studie II zu immer demselben Ergebnis führen (deterministisch), während bei Williams Mix aus jedem Durchlauf des Programms eine andere Realisierung des Konzepts Williams Mix entsteht.
62 Was wiederum tiefere Fragen zur Verrücktheit oder Vernünftigkeit von Wissenschaft berührt. Man denkt an das berühmte Zitat einer durch Borges zitierten angeblichen oder wirklichen chinesischen Enzyklopädie am Anfang von Foucaults Ordnung der Dinge, in der Tiere so gruppiert werden: „a) Tiere, die dem Kaiser gehören, b) einbalsamierte Tiere, c) gezähmte, d) Milchschweine, e) Sirenen, f) Fabeltiere, g) herrenlose Hunde, h) in diese Gruppierung gehörige, i) die sich wie Tolle gebärden, k) die mit einem ganz feinen Pinsel aus Kamelhaar gezeichnet sind, l) und so weiter, m) die den Wasserkrug zerbrochen haben, n) die von weitem wie Fliegen aussehen.“ (Michel Foucault, Die Ordnung der Dinge, Frankfurt 1974, S. 17)
63 I Ging (dessen Verfahren zur Auswahl Cage aufnimmt) heisst soviel wie „Buch der Wendungen“. Im Vorwort zu den Variations II heisst es: „If, to determine this number [gemeint zunächst die number of readings eines Musters aus Punkten und Geraden] a question arises or if questions arise regarding other matters or details (e.g. is one of the parts of a constellation itself a constellation, or aggregate), put the question in such a way that it can be answered by measurement of a dropped perpendicular.“ Wenn das keine Wendung eines orakelhaften Denkens und Vorgehens ist ... (John Cage, Variations II, Henmar Press New York 1961)
64 Siehe Tabelle B „Frequenzen Tongemische“ in der Einleitung zur Partitur (Seite V).
65 Ein Transpositionsfaktor von 1 führt zu einer Auswahl unter den Gruppen 1-5, ein Transpositionsfaktor von 2 führt zu einer Auswahl unter den Gruppen 2-6, und so weiter bis zum Transpositionsfaktor 5, der zur Auswahl unter den Gruppen 5-9 führt.
66 Der Vorgang des Änderns lässt sich in den Skizzen (besser eigentlich als Arbeitspartitur zu bezeichnen) sehr schön nachvollziehen. Stockhausen hatte schon eine große "1" für die Transposition geschrieben; nun widmet er eine der vorherigen Spalten um und nennt sie "Tr." (für Transposition). Vergleiche die Originalabbildung, die ich dank der Freundlichkeit der Stockhausen-Stiftung auf der Linux-Audio-Konferenz 2010 im Faksimile zeigen konnte: http://lac.linuxaudio.org/2010/download/JHeintz.pdf (Folie 15)
67 Es heisst ja nur etwas wie: „Wenn wir im dritten Teil sind, entstehen die Tondauern nach Regel X; wenn wir im vierten Teil sind, nach Regel Y.“
68 Siehe Folie 14 in dem oben (Anm. 64) genannten pdf (LAC 2010).
69 In meiner Nachprogrammierung hat der dritte Teil 13 Zeilen Code, der fünfte Teil dagegen 94 ...
70 Wenn man also eine algorithmische Komposition hört, bei der die Weile zur Langeweile wird, kann es entweder daran liegen, dass die Idee diese Langeweile hat, oder am Algorithmus nicht so gearbeitet wurde, dass er die Idee erreicht.
71 Beide Komponisten arbeiteten an diesen kurzen Stücken etwa ein Jahr.